Blaise Pascal
Impulsado por su padre, Blaise Pascal se adentra en la geometría y las matemáticas con tan solo 12 años, lo que lo convierte en un genio precoz que tuvo gran influencia en el siglo XVII con notables inventos tales como el desarrollar una maquina para sumar y el triángulo aritmético que hoy conocemos como Triángulo de Pascal.Triángulo de Pascal o Triángulo de Tartaglia (da click aquí para ver un video del tema)
Es una tabla numerica infinita de forma triangular que nos permite resolver toda una gama de problemas de calculo.Propiedades
- Todas las filas empiezan y acaban en 1.
- El vértice superior comienza en 1.
- Para obtener los siguientes renglones siempre vamos a sumar los números que estén uno al lado del otro tomando como termino general: (a+b)^n. Por ejemplo, para obtener el 2 que está en el tercer renglón sumamos a+b que en este caso son 1+1 del segundo renglón.
- El termino general que se usa durante la elaboración del triangulo es: (a+b)^n.
Los números que arroja (coeficientes) el artificio matemático del triángulo de Pascal se colocan aparte y a estos se les agrega las literales que me proporciona el problema y colocando las potencias en contrasentido, es decir, primero colocamos las potencias de izquierda a derecha para la primera literal y después de derecha a izquierda para la segunda literal.
Por ejemplo.
- En este caso, los coeficientes son:
1 5 10 10 5 1
- Escribimos la primera literal que es x a un lado de cada coeficiente.
1x 5x 10x 10x 5x 1x
- Ahora vamos a escribir los exponentes de esas literales. Empezamos con el exponente al cual estamos elevando el binomio, en este caso, 5, y conforme avanzamos a la derecha, exponentes van disminuyendo, uno en cada literal.
- Escribimos la otra literal, a junto a cada literal x:
- Le ponemos exponente a las letra a.
- El paso siguiente es colocar los signos + entre los términos, quedando como:
Binomio de Newton
Una de las razones de la importancia del Triángulo de Pascal o de Tartaglia, es
su relación con el BINOMIO DE NEWTON que permite un rápido y fácil cálculo de
binomios elevados a cualquier exponente natural utilizando la formula:
Este toma de referencia los coeficientes del Triángulo de Pascal para determinar el desarrollo de la potencia requerída.
Por ejemplo.
Ten en cuenta que...
- Los denominadores, de acuerdo a la formula, irán del 0 hasta n (que en este caso es 4).
- Con forme k aumenta, n disminuye.
AYUDA
Te dejo a continuación unos videos que espero sean de ayuda para reforzar los anterior.
Referencias
- http://www.estadisticaparatodos.es/taller/triangulo/triangulo.html
- https://es.scribd.com/doc/42385386/Triangulo-de-Pascal
- http://centros5.pntic.mec.es/~marque12/matem/tripasca.htm
- http://www.aprendematematicas.org.mx/notas/algebra/DGB1_2_5.pdf
- http://www.vitutor.com/pro/1/a_n.html





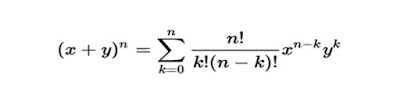

Muy buena información, explicas pasó a pasó y de manera clara, como se debe elaborar y los vídeos que incluiste son una buena herramienta para comprender mejor el tema.
ResponderEliminarGracias, que gusto saber que lograste entender el tema de manera clara, saludos.
EliminarEl ejemplo usado fue de gran ayuda a la hora de implementarlo en un ejercicio, es un tema algo complicado y fue de gran ayuda las explicaciones y los videos para lograr un mejor entendimiento del tema y sus usos.
ResponderEliminarCiertamente es un tema un tanto complicado y un poco extenso, sin embargo, traté de plantearlo lo más fácil posible de entender. Gracias por tu comentario, saludos.
EliminarMuy buena explicación
ResponderEliminarGracias, saludos.
EliminarMe pareció interesante la manera que explicaste un tema con un grado de dificultad como este y el video fue de gran ayuda
ResponderEliminarMuchas gracias, me alegra que haya agradado el video, ya que sirve de apoyo para resolver cualquier duda que hubiese quedado. Saludos.
Eliminarme gustó como ordenaste y explicaste la información, este es un tema muy difícil de explicar pero tu tuviste muy buen genio para explicarlo
ResponderEliminarGracias por leer mi blog. Realmente para mi fue un tanto difícil el tema, pero después de practica logre comprenderlo y hacer este blog de la forma más explícita posible. Saludos.
Eliminarme gustó como ordenaste el blog y tu diseño, sigue así. :)
ResponderEliminarGracias, me alegra que te haya gustado y servido. Te invito a seguir frecuentando mi blog, saludos.
EliminarEl diseño me gusto mucho, y la forma en la que lo ordenaste me facilita su compresión. Ademas que los vídeos e imágenes fueron de gran ayuda.
ResponderEliminarGracias, es bueno saber que fue de tu agrado y que lograste captar lo que quise explicar de la manera más clara, saludos.
EliminarBuena información es clara y ayuda aclarar mis dudas el diseño es fantástico sigue así!!!
ResponderEliminarMuchas gracias Roberto, me alegra que te haya gustado, saludos.
EliminarMuy buen blog Julieta☺️ todo bien explicado y ordenado, además el diseño es muy lindo, sigue así!
ResponderEliminarGracias por comentar, saludos.
Eliminar