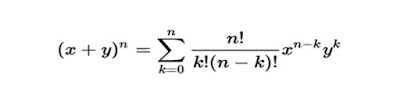Triángulo de Pascal

Blaise Pascal

Impulsado por su padre, Blaise Pascal se adentra en la geometría y las matemáticas con tan solo 12 años, lo que lo convierte en un genio precoz que tuvo gran influencia en el siglo XVII con notables inventos tales como el desarrollar una maquina para sumar y el triángulo aritmético que hoy conocemos como Triángulo de Pascal.

Triángulo de Pascal o Triángulo de Tartaglia (da click aquí para ver un video del tema)

Es una tabla numerica infinita de forma triangular que nos permite resolver toda una gama de problemas de calculo. 

Propiedades

1. Todas las filas empiezan y acaban en 1.
2. El vértice superior comienza en 1.
3. Para obtener los siguientes renglones siempre vamos a sumar los números que estén uno al lado del otro tomando como termino general: (a+b)^n. Por ejemplo, para obtener el 2 que está en el tercer renglón sumamos a+b que en este caso son 1+1 del segundo renglón.
4. El termino general que se usa durante la elaboración del triangulo es: (a+b)^n.  

Una forma sencilla de encontrar los coeficientes del resultado de elevar el binomio (x + a)^n.
Los números que arroja (coeficientes) el artificio matemático del triángulo de Pascal se colocan aparte y a estos se les agrega las literales que me proporciona el problema y colocando las potencias en contrasentido, es decir, primero colocamos las potencias de izquierda a derecha para la primera literal y después de derecha a izquierda para la segunda literal.
Por ejemplo.

•  En este caso, los coeficientes son: 

1   5    10   10   5   1 

• Escribimos la primera literal que es x a un lado de cada coeficiente. 

1x   5x   10x   10x   5x   1x  

• Ahora vamos a escribir los exponentes de esas literales. Empezamos con el exponente al cual estamos elevando el binomio, en este caso, 5, y conforme avanzamos a la derecha, exponentes van disminuyendo, uno en cada literal.

• Escribimos la otra literal, a junto a cada literal x:

• Le ponemos exponente a las letra a.

• El paso siguiente es colocar los signos + entre los términos, quedando como: 

Binomio de Newton

Una de las razones de la importancia del Triángulo de Pascal o de Tartaglia, es su relación con el BINOMIO DE NEWTON que permite un rápido y fácil cálculo de binomios elevados a cualquier exponente natural utilizando la formula: 

Este toma de referencia los coeficientes del Triángulo de Pascal para determinar el desarrollo de la potencia requerída.

Por ejemplo.

Ten en cuenta que...

• Los denominadores, de acuerdo a la formula, irán del 0 hasta n (que en este caso es 4).
• Con forme k aumenta, n disminuye.

AYUDA

Te dejo a continuación unos videos que espero sean de ayuda para reforzar los anterior.

Referencias

• http://www.estadisticaparatodos.es/taller/triangulo/triangulo.html
• https://es.scribd.com/doc/42385386/Triangulo-de-Pascal
• http://centros5.pntic.mec.es/~marque12/matem/tripasca.htm
• http://www.aprendematematicas.org.mx/notas/algebra/DGB1_2_5.pdf
• http://www.vitutor.com/pro/1/a_n.html

Operaciones con polinomios

El prefijo poli significa “muchos”. Polinomio significa entonces “muchos términos”. 

Un polinomio es una expresión algebraica que está conformada por: constantes, variables y exponentes, estos, se encuentran combinados usando sumas, restas y multiplicaciones.

Las características principales de estos son:

1. El polinomio más sencillo es aquel que tiene un término y se lo llama Monomio.
2. Si un polinomio tiene dos términos, se llama BINOMIO.
3. A partir de cinco términos, se los llama, POLINOMIO DE , cinco, seis, siete, etc. términos.

Ejemplo.

Muchas veces, solo con el simple hecho de mirar las literales y los exponentes pensamos que será algo difícil de realizar, sin embargo, si bien no es un proceso complicado, es un poco largo pero que, con la práctica, lograrás dominar rápidamente.

Multiplicación

Para multiplicar los polinomios, primero debemos de llevar un orden, es decir, comenzar con el primer termino siempre y operar de manera distributiva a los demás términos de acuerdo a el termino primero.

Toma este ejemplo para poder darte una idea.

(2x+4) (3x^2-4x)

=2x(3x^2-4x)+4(3x^2-4x)

=6x^3-8x^2+12x^2-16x

=6x^3+4x^2-16x

Suma

Para realizar una suma de polinomios, el primer paso a realizar es visualizar los términos y eliminar los paréntesis, ¿cómo?, multiplicando por el signo que se encuentra a fuera del paréntesis.

Comencemos con un ejemplo para que hagamos esto paso a paso.

(7x-10x)+(8+5x)-(+y-3x^2+x)

=7x-10x+8x+5x-x+3x^2-x

Recuerda

Cada que afuera de un paréntesis existe el signo +, todo el termino quedará igual. Si hay un signo -, todos los signos cambian.

Ahora bien, continuando con la suma. El paso siguiente que debemos realizar es el de reducir términos, en otras palabras, debemos buscar todos los números con la misma literal y sumarlos algebraicamente.

=7x-10x+8x+5x-x+3x^2-x

= (7+5-1)= 11x -(-10+8-1)= -3x 

=11x-3x+3x^2

Recuerda

• Cuando una literal no tiene letra, se interpreta como si tuviese un 1.
• Si existe un término único, simplemente se pasa igual.

Resta

Primero que nada, al igual que en la suma, lo primero que debemos hacer es eliminar los paréntesis de igual forma.

(5x-1)-(2-3x)

=5x-1-2+3x

=8x-3

Recuerda

El resultado debe organizarse de manera ascendente o descendente, es decir, de el mayor al menor o de el menor al mayor.

División

Consiste en hallar uno de los factores de un producto, que recibe el nombre de cociente dado el otro factor, llamado divisor, y el producto de ambos factores llamado dividendo.

Teorema fundamental de la aritmética

Números primos (da click aquí para saber más del tema) 
Un número es considerado primo cuando es entero positivo, distinto de 0 y 1 y que únicamente se puede dividir por sí mismo y por 1 para dar una solución exacta. Entonces, este teorema declara que “Todo entero positivo puede descomponerse de manera única como un producto de números primos”.

Números compuestos 
Un número compuesto es aquel que es divisible por otros números que no sean 1 o el mismo. En otras palabras, tiene más factores que 1 y sí mismo.

Entonces, desarrollemos el teorema. 
Este teorema, dictado por Euclides, expone que todo número puede dividirse una y otra vez hasta llegar a un grupo pequeño de números iguales, siendo estos los números primos.
Tomando como referencia a los números primos como bloques de construcción; no importa cual sea el número que se elija, siempre se puede construir dicho número una adición de números primos.
Ahora bien, si buscamos todos los factores en los que se puede dividir cierta cantidad y los multiplicamos entre sí, esto nos dará el número original, a esto se le llama factorización prima. No existe otra manera de construir este número de diferente forma.
Ejemplo.