Instituto Patria Nueva
Determinante de Gauss
"Matemáticas III"
Prof. Marco Antonio Morales Contreras.
Julieta López Jiménez.
3°B BACHILLERATO.
31/08/2017. Villahermosa, Tab.
Determinante de Gauss, herramienta para la graficación de polígonos.
Dadas las coordenadas de un polígono formado en el plano cartesiano se puede determinar su área por el método determinante de Gauss y su perímetro por la fórmula de la distancia entre dos puntos.
Conocido también como el método de lazada debido al constante cruce de operaciones parecido al de los lazados de los tenis, es un método práctico para calcular cualquier área de polígono ya que su fórmula es bastante sencilla de comprender (si se lleva a cabo correctamente el procedimiento) y poco extensa.
Área
Para poder calcular el área del polígono se debe tomar de base principalmente la fórmula que Gauss proporciona:
1. Se forma el determinante (las dos columnas) con las coordenadas de lo vértices del polígono, considerando un orden igual al del giro de las manecillas del reloj.
2. Se procede a multiplicar cruzadamente sumando cada uno de los resultados. Tomando en cuenta que la primera coordenada se debe poner dos veces: al principio y al final de la matriz (así como se muestra en el ejemplo de abajo).
= (2(2)+ 1(1)+ 4(3))
(-3(1)+ 2(4)+ 1(2))
=(4+1+12)
=-(3+8+2)
= 1/2 |17-13| = |4|
3. Ahora, debes dividir el resultado de tu determinante entre dos. La unidad de tu resultado será u^2.
= 4/2= 2u^2
Perímetro
Ahora bien, tomando como referencia el mismo polígono, debemos de calcular cada uno de los segmentos formados en el polígono para así poder obtener su perímetro.
De manera que primero debemos determinar cuál será el segmento que se calculará primero. Mi referencia será el segmento AB.
La fórmula general para realizar este procedimiento es la siguiente:
Esta fórmula nace debido a que al proyectar los puntos de un segmento y generar un triangulo rectángulo podemos despejar el teorema de Pitágoras para este tipo de situaciones, sin embargo, no necesariamente debe ser un triángulo rectángulo para poder utilizar este procedimiento, es por eso que es una formula general.
Sustituimos los valores, combinandolos de la siguiente forma:
Lo siguiente seria despejar la fórmula, tratando de dejar los resultados en raíz para evitarnos los decimales periódicos.
Posteriormente, debemos realizar dicha operación con cada uno de los segmentos:
Finalmente, debemos sumar el resultado de los rayos para así poder obtener el perímetro que es igual al contorno de toda la figura.
Muchas veces podemos llegar a creer que un problema es sumamente difícil cuando vemos el algoritmo que debemos llevar, sin embargo cuando logras analizarlo correctamente y conectar tus ideas comprendes el tema y por consiguiente podrás llevarlo a la práctica.
Entonces, al conocer estos métodos podremos determinar el área y perímetro de cualquier polígono ya que estas son fórmulas generales para cualquier situación.
Si crees que necesitas repasar el tema una vez más, te invito a que visites los siguientes links como sugerencia mía.
REFERENCIAS
- Desconocido. (Desconocido de Desconocido de Desconocido). Matrices, determinantes y sistemas de ecuaciones. Obtenido de Universidad de granada: http://www.ugr.es/~mmartins/docencia/Biotec/M1_T1.pdf
- García., P. F. (16 de Marzo de 2011). CÁLCULO DEL ÁREA DE UN POLÍGONO. Obtenido de Scribd: https://es.scribd.com/doc/50892425/CALCULO-DEL-AREA-DE-UN-POLIGONO
- Gerarjam. (18 de Septiembre de 2009). Área de polígonos . Obtenido de Slide share: https://es.slideshare.net/gerarjam/rea-de-polgonos-2020579
- MateFacil. (14 de Julio de 2016). 08. Perímetro de un triángulo en el plano cartesiano (con gráfica y fórmula de distancia). Obtenido de Youtube: https://www.youtube.com/watch?v=pGDsRSooBY0
- Quidiello, M. J. (05 de Octubre de 2013). Determinante de una matriz por el método de Gauss. Obtenido de Youtube: https://www.youtube.com/watch?v=4A1igGh05FM







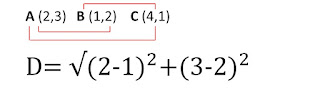



Muy buena explicación y este tema comparando el de Herón para mí es muy fácil, sigue así 👍
ResponderEliminarGracias, te invito a que sigas frecuentando mi blog.
EliminarExcelente post,me encanto, explicaste detalladamente los pasos para realizar el método de Gauss,sigue así, saludos.
ResponderEliminarMe da gusto que te haya gustado y haya sido de ayuda, te invito a que sigas frecuentando mi blog.
EliminarMuy buena información, igual das una buena explicación del tema y las imágenes ayudan mucho👌🏻, me gusto, te invito a pasarte por mi blog.
ResponderEliminarMuchas gracias, te aseguro que me pasaré por tu blog.
EliminarPersonalmente es un tema sencillo de comprender y con la informacion que expusiste pude hacerlo.
ResponderEliminarGracias por comentar, es grato saber que fue de tu comprensión y ayuda, te invito a que sigas frecuentandome.
EliminarEst muy padre tu blog,ya logre comprender bien esta tema,gracias a tu informacion
ResponderEliminarQue bueno que lograste comprenderlo Dylan, te invito a que sigas visitando mi blog para más post como este.
EliminarMuy buen blog ,solo que es mucha información que digerir,recomendaria poner un video
ResponderEliminarGracias por tu sugerencia Max, sin embargo, en la parte de abajo adjunté 4 videos.
EliminarGracias a tu investigación pude reforzar lo que vimos en clases y así al hacerlo otra vez ya no me salgan mal mis operaciones.
ResponderEliminarEs bueno saber que has logrado comprender el tema Iris, si te gustó te invito a que sigas frecuentando mi blog para más publicaciones cómo está.
EliminarMuy bien tu blog, me gusto mucho la manera en la que explicaste el metodo de Gauss, toda la información es muy buena y los ejemplos que pusiste también lo son. Bien hecho.
ResponderEliminarGracias por comentar, saludos :)
EliminarTu blog es bueno, tu información esta bien explicada y gracias a eso es fácil de entender felicidades.
ResponderEliminar